An $n$th-rank tensor in $m$-dimensional space is a mathematical object
that has $n$ indices and $m^n$ components and obeys certain transformation
rules.
Each index of a tensor ranges over the number of dimensions of space.
Chaoran Huang, UNSW Sydney.
Presenter: Chaoran Huang
chaoran.huang@unsw.edu.au


An $n$th-rank tensor in $m$-dimensional space is a mathematical object
that has $n$ indices and $m^n$ components and obeys certain transformation
rules.
Each index of a tensor ranges over the number of dimensions of space.
$0$-rank tensor: Scalar
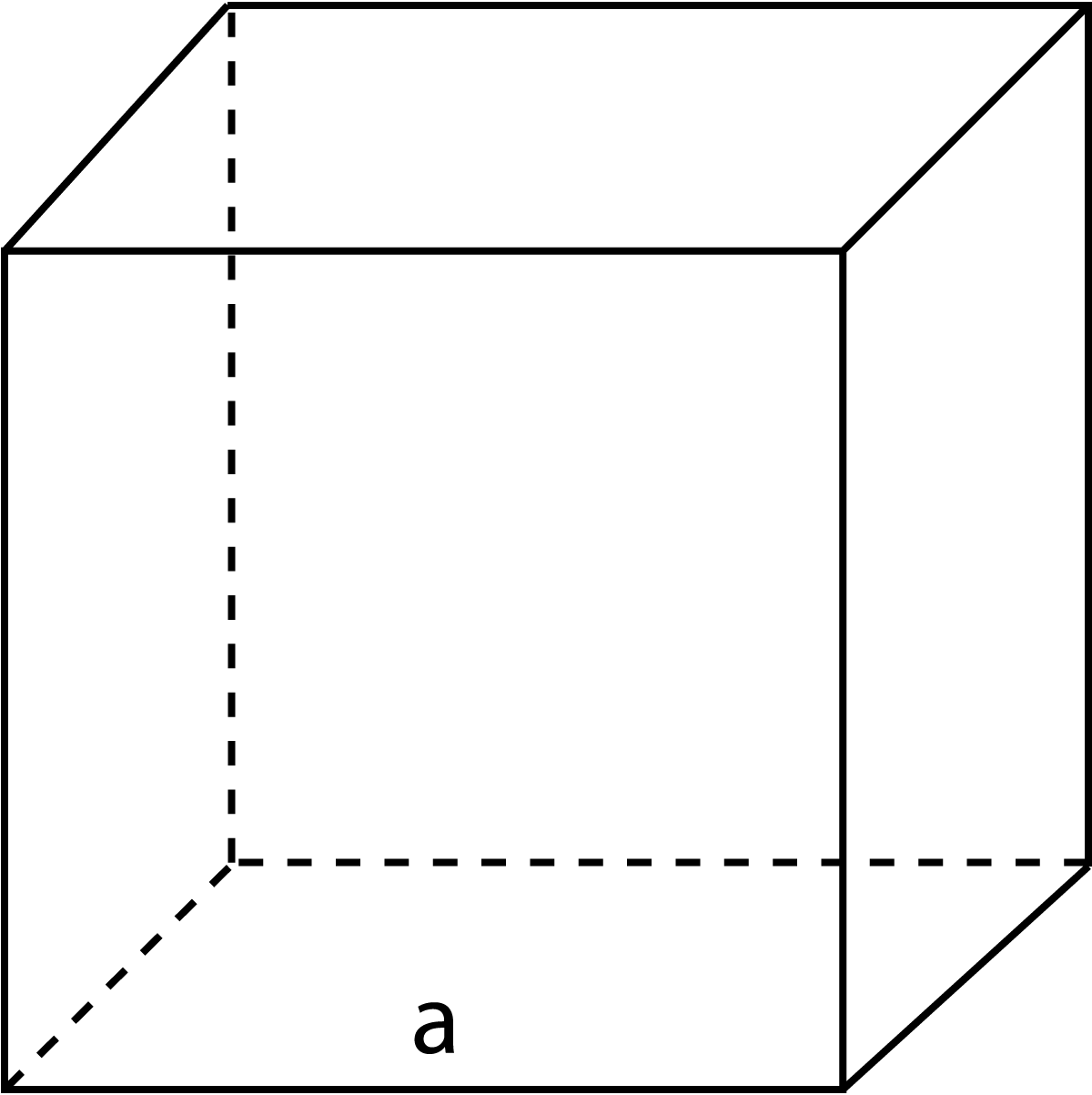
Magnitude
length: $a$; Volume: $a^3$
$1$st-rank tensor: Vector
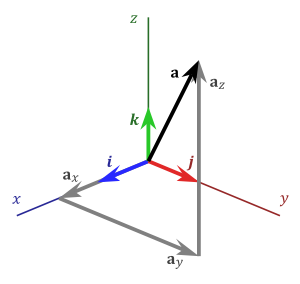
Magnitude, direction
$2$nd-rank tensor: Dyadic (Dyad)
$3$rd-rank tensor: Triad
$4$th-rank tensor: Quartad
$n$th-rank tensor: $n$-th-ad
Kronecker Product
Khatri-Rao Product(a.k.a matching columnwise Kronecker Product)
Hadamard Product(elementwise product)
Interesting Property
Fibers and Slices
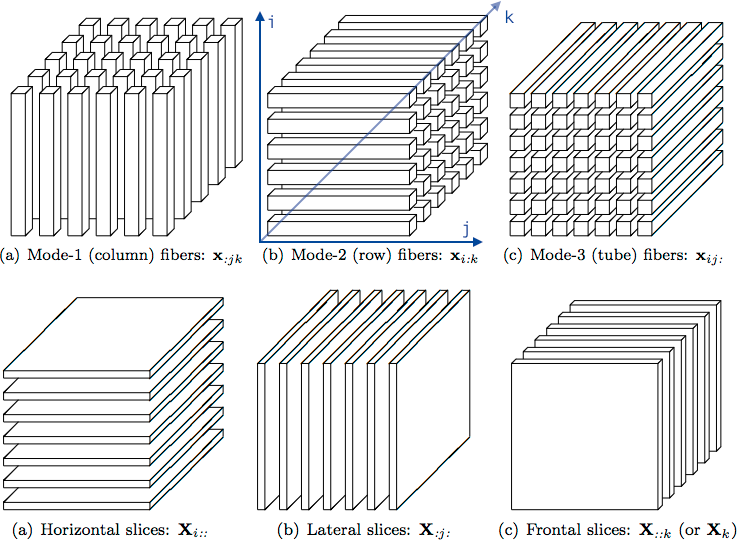
Matricization(unfolding)
Example
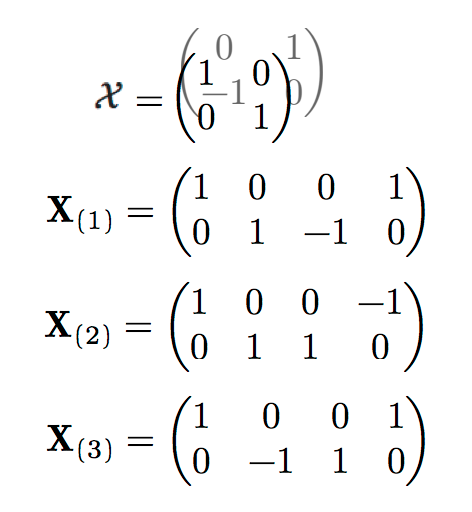
Example(contiune)
modes
Review of Matrix Factoriztion
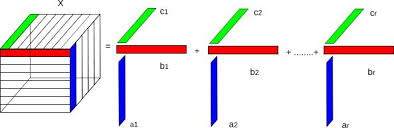
Different names of CANDECOMP/ PARAFAC Decomposition
| Name | Source |
|---|---|
| Polyadic Form of a Tensor | Hitchcock, 1927 |
| PARAFAC (Parallel Factors) | Harshman, 1970 |
| CANDECOMP or CAND (Canonical decomposition) | Carroll and Chang, 1970 |
| Topographic Components Model | Möcks, 1988 |
| CP (CANDECOMP/PARAFAC) | Kiers, 2000 |
Why the sudden fascination with tensors?
- Videos;
- Complex subject-items relationships;
- ...
- Google Tensor Processing Unit (TPU)/ 28-40 W @ 45 TFlops
- NVIDIA® Tesla® V100/ 300W @ 120 TFlops
The modal unfoldings
The modal unfoldings(continue)
Computing the CP Decomposition(Alternating Least Square)

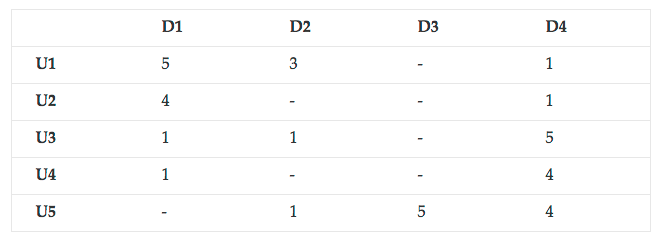
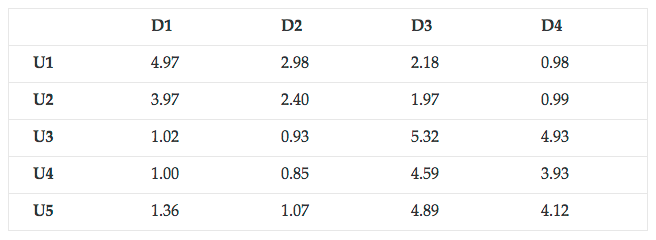
Tensor Factorization based Expert Recommendation
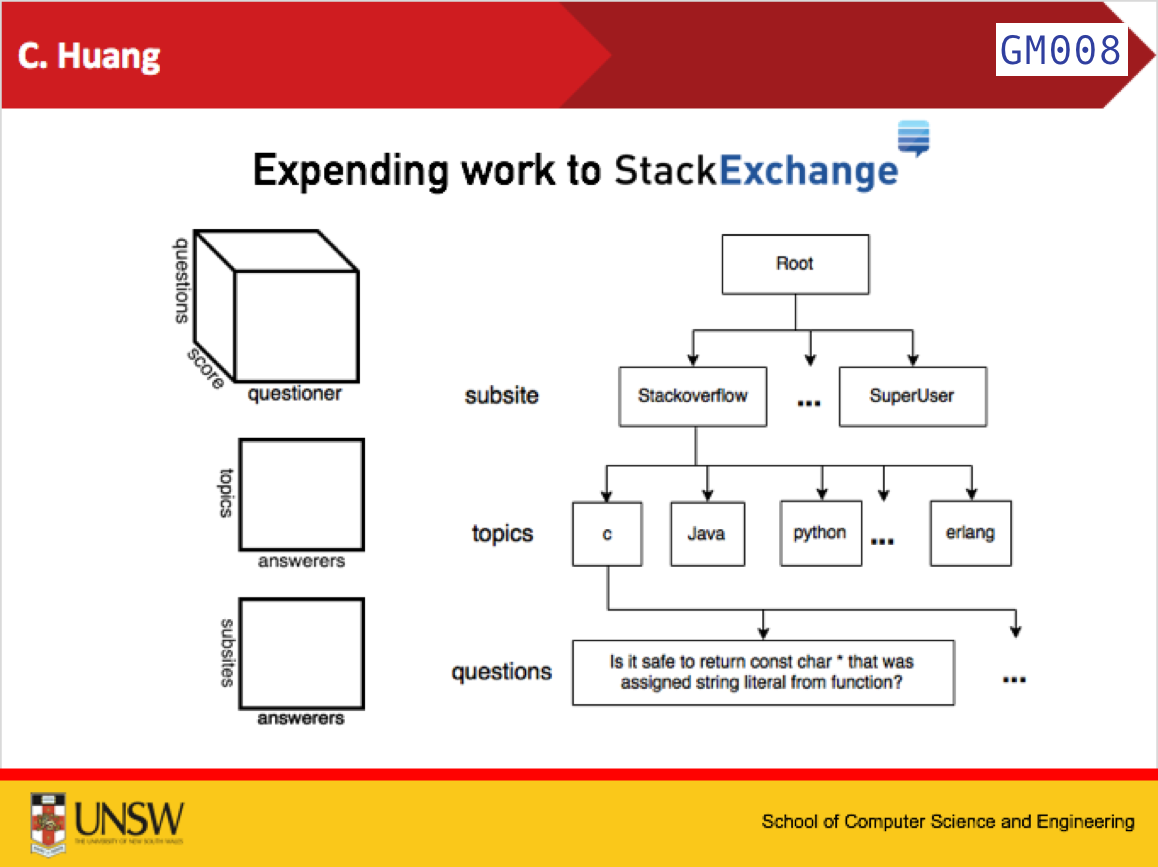

Chaoran Huang, 19 Jun., 2017
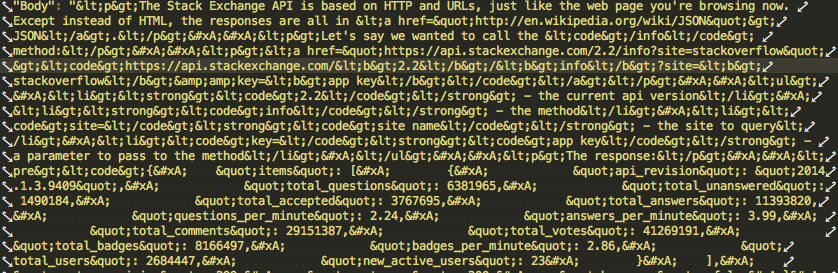
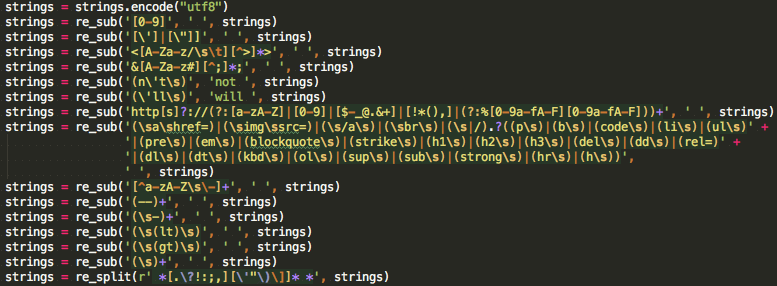
- 98 GiB plain text...
- Bad formatted texts...
- almost finished
- est. 3200 CPU hrs/40 threads
@ 24k words/thread/sec
- Expanding methodology - Waiting for language model - Implementing algorithms